Der Übergang vom Abakus zum heutigen Taschenrechner verlief langsam, aber dazwischen gab es Erfindungen wie die „Napier-Knochen”, die den Zugang zu komplexer Mathematik revolutionierten. Der Name John Napier sagt Ihnen vielleicht nichts, aber ich kann Ihnen versichern, dass Sie ihn höchstwahrscheinlich nicht mögen würden. Denn was Ihnen vielleicht bekannt ist, sind die Napier-Logarithmen, die uns in der Schule so viele Kopfschmerzen bereitet haben. Napier war es, der diese Funktion zum ersten Mal definierte, aber um das „auszugleichen”, schuf er auch das, was wir als Vorläufer des heutigen Taschenrechners betrachten können.
Etwas namens „Napier-Bones”, das wie Dominosteine aussieht, aber mehr Menschen an mathematische Operationen heranführte.
John Napier. Dieser Schotte interessierte sich für viele Dinge. Seine Familie war mehr als wohlhabend, und als Sohn einer wohlhabenden Familie besuchte er im Alter von 13 Jahren die Universität von Saint Andrews. Er blieb nicht lange dort, aber nicht, weil er sein Studium abbrechen wollte, sondern weil er an andere Universitäten in Frankreich, Italien oder Flandern ging. Er verbrachte sein Leben damit, von Schloss zu Schloss zu ziehen, wo er mehreren seiner Leidenschaften freien Lauf ließ.

Ein Zauberer (aber kein Zahlenzauberer). Er war Protestant und wurde von seinen Nachbarn als schwarzer Magier angesehen. Er war auch ein findiger Kerl. Als die Tauben sein Getreide fraßen, beschloss er, mit Alkohol getränkte Samen auf dem Feld zu verstreuen, und als die Tauben „betäubt” und flugunfähig waren, fing er sie ein. Wie immer, und umso mehr, wenn es um solche Geschichten geht, die mehrere Jahrhunderte zurückliegen, spielen Fantasie und Übertreibung eine Rolle, aber es ist unbestreitbar, dass Napier gerne Probleme löste.
Sein größter Beitrag ist das erwähnte Mirifici Logarithmorum Canonis Descriptio, in dem er 1614 die heutigen Logarithmen definierte, aber davor und danach veröffentlichte er weitere Abhandlungen auf dem Gebiet der Mathematik, in denen er Möglichkeiten zur Vereinfachung von Rechenaufgaben untersuchte. Und er theoretisierte nicht nur darüber oder förderte die Verwendung des Dezimalpunkts, sondern schuf auch Werkzeuge, um diese Berechnungen einfacher zu lösen.

Der neue Abakus. Seitdem wir mathematische Probleme lösen müssen, hat die Menschheit nach Möglichkeiten gesucht, sich auf Hilfsmittel zu stützen. So entstanden Abakusse oder Quipus, mit denen einfache Rechenoperationen wie Addition, Subtraktion und Multiplikation durchgeführt werden konnten. Mit komplexeren mathematischen Aufgaben musste das System überarbeitet werden, und Napier entwickelte seinen neuen Abakus oder einen Prototyp eines Taschenrechners.
Napiers Knochen. Im Jahr 1617, kurz vor seinem Tod, erfand der Mathematiker ein manuelles Werkzeug, das einige komplexere Rechenoperationen wie Multiplikation und Division, aber auch Quadratwurzeln erleichtern sollte. Es handelte sich um einen Satz rechteckiger Stäbe, auf denen die Multiplikationstabellen eingraviert waren, sowie um ein Brett mit Aussparungen für die Stäbe und den Zahlen von 1 bis 9, die vertikal auf der linken Seite angeordnet waren.
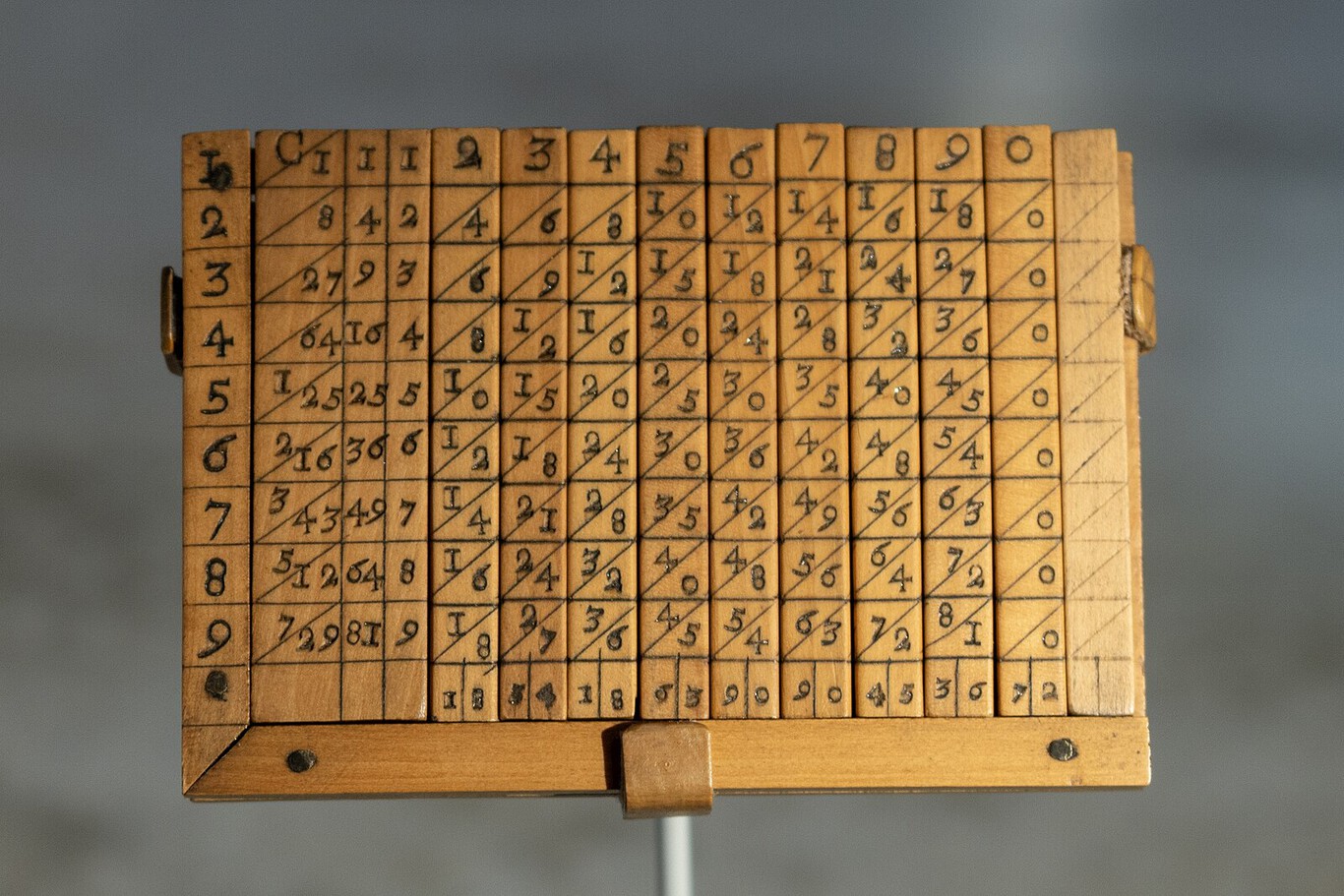
Durch das Aneinanderreihen dieser Stäbe wurden Multiplikations- und Divisionsoperationen auf einfache Additionen bzw. Subtraktionen reduziert. Ursprünglich wurden sie vor allem aus Metall oder Holz hergestellt, aber diese Stäbe konnten auch aus Elfenbein gefertigt werden, und ein komplettes Spiel umfasste 10 Stäbe, die die Zahlen von 0 bis 9 darstellten.
Was? Okay, wie in der Mathematik üblich, schauen wir uns Beispiele an. Ein sehr einfaches Beispiel ist die Multiplikation, denn so müssen wir uns die Tabellen nicht merken. Wenn wir wissen wollen, wie viel 2 x 6 ist, suchen wir einfach die zweite Reihe von rechts und den Stab, der mit 6 beginnt, und sehen, welche Zahl im Quadranten steht: die 12. Wenn wir 8 x 8 rechnen wollen, wiederholen wir den Vorgang und sehen, dass wir 64 erhalten.
Wenn wir eine komplexere Rechnung durchführen, wie z. B. 46785399 x 7, legen wir die Stäbe, die dieser Zahl entsprechen (den, der mit 4 beginnt, den, der mit 6 beginnt, und so weiter), nebeneinander von links nach rechts und schauen auf die Zahl in der Reihe 7, mit der wir multiplizieren wollen.
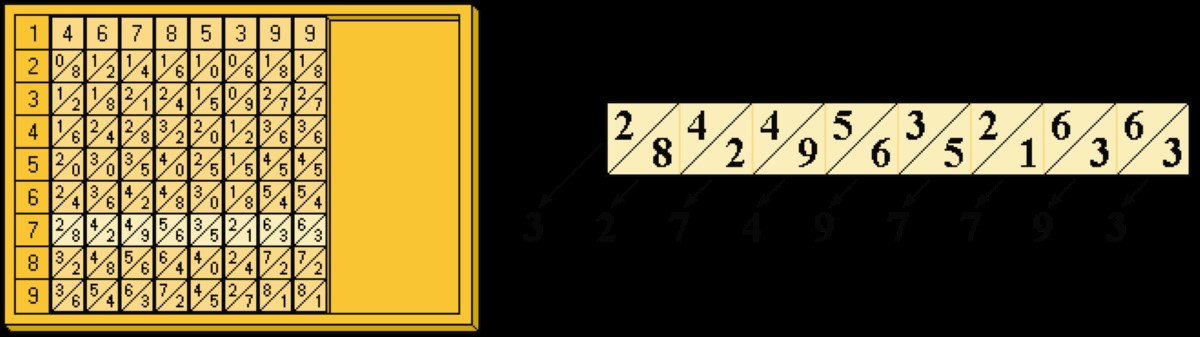
Nun legen wir von rechts nach links die Zahlen, die in dem diagonalen Feld erscheinen, nebeneinander: 327497793. Spätere Mathematiker verbesserten das System, indem sie ein Brett mit einer Neigung von 65° entwickelten, das die visuelle Identifizierung dieser Formel verbesserte, aber die „Napier-Knochen” waren eine Revolution, da sie diese komplexere mathematische Berechnung auch Menschen ohne höhere Bildung zugänglich machten. Das Einzige, was man lernen musste, war.









